Discussions

 

In this section, we discussed functionalities of and mutual dependencies between perception, action, and communication. While some important observations were derived, the presented model is very naive and needs to be improved in the following points:

1. includes various different types of information: one which affects the perception (e.g. camera parameters), one defining the state of a physical body, one describing the perceived world state, one representing knowledge, and so on. To refine the model, we should first categorize into a set of sub-states depending on the types of information represented. Such state categorization will make the models of perception, action, and communication refined and will lead us to a more sophisticated internal architecture of an AVA.
2. The most critical limitation of the current model is that it only represents static functional dependencies and no dynamic properties are taken into account. To augment the model by introducing temporal characteristics (e.g. temporal order, synchronization, and time-out) is crucial to investigate the integration of perception, action, and communication. Without such augmentation, the cooperation among AVAs cannot be realized or intelligence does not emerge.
3. The above two augmentations are still not enough to model AVAs which can work persistently in the real world; since failures, errors, and noise are ubiquitous in the real world, we should introduce their models into the overall AVA model.

As a step toward the complete AVA model with these points into account, Asada[15], a core member of the project, proposed the following linear dynamic system to model an embodied AVA without message exchange capability. In what follows, we will discuss its characteristics and limitations to clarify the state-of-the-art and future technical problems.

  

where , , and denote n dimensional state vector, m dimensional action code vector, and q dimensional percept vector, respectively. and represent n and q dimensional noise vectors respectively.

Equation (11) represents a practical implementation of equations (7) and (8). Note that in equation (11), the action code vector is introduced as an descriptive embodiment of the action, while in equations (7) and (8), the action is modeled as a mapping function.

Comparing equations (1) and (12), in the former is replaced with in the latter. This means that the above linear model assumes that the AVA's action is directly and immediately reflected onto its percept. This assumption implies the elimination of the world state and hence the neglection of the information flow from ActionToWorld to Perception via illustrated in Fig. 6. Consequently, the applicability of the model is limited to rather simple worlds. To cope with this limitation, Asada applied the model to each object in the world; different linear models were prepared for different objects in the world.

The above linear model has a more crucial limitation. It basically considers as input and as output. That is, while the model represents how AVA's action is reflected onto the percept (i.e. action-driven perception process), its reciprocative process, i.e. how the percept is used to change the state and then select the action (i.e. perception-driven state-change process followed by action-selection process), is not modeled explicitly. To compensate this limitation, a pair of functions to map percept into state and then state into action were incorporated. The former function is described by a transformation matrix analytically derived by Canonical Variate Analysis. The latter function, on the other hand, is represented by an associative memory where tuples of ( ) are stored. This representation is acquired from training data through Q learning and allows the flexible activation of actions depending on the internal state.

Finally we should note the meaning of the state. In the above linear system, the state vector represents the instantaneous state, while we used means the persistent state denoting the memory. That is, equations (11) and (12) merely define a filter function without memory. We believe that AVAs should have memories to work adaptively to a wide spectrum of situations in the real world. In fact, Asada extended the input and output vectors of the system into the followings to characterize temporal features during a certain length of time period.

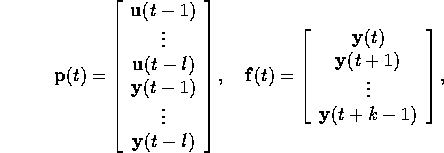
Note that these extended vectors really model the first-in-first-out memories (i.e. queues) of size l and k respectively.

As is shown in the discussions given in this section, our study to explore the integration of perception, action, and communication has only made a little step forward. Deep considerations over a wide spectrum of different disciplines including control theory, software science, psychology, and linguistics are required to complete the model.