


Next: 実験
Up: カメラを搭載したロボットと対象物体の運動の同時制御
Previous: カメラを搭載したロボットと対象物体の運動の同時制御
Contents
本研究においては, 画像を各画素値を座標値とする, 総画素数Nの次元の空
間の一点Iで表し, そのS次元部分空間の基底
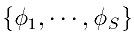 とIの内積をとることで得られるベクトルa'
(図2.34(a))をカメラ・対象物体の運動と対応つけることで視
覚サーボを行う.
カメラ・対象物体の位置・姿勢をwで表す. wの運動に
対する
a'の変化の関係は, 行列LTを用いて,
とIの内積をとることで得られるベクトルa'
(図2.34(a))をカメラ・対象物体の運動と対応つけることで視
覚サーボを行う.
カメラ・対象物体の位置・姿勢をwで表す. wの運動に
対する
a'の変化の関係は, 行列LTを用いて,
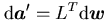 |
(2.4) |
と記述される. LTは相互行列と呼ばれる. LTはwの値に依存
するが,制御を容易に実現するためには, LTが一定とおけることが望ましい.
そこで, ゴール近傍のなるべく広い範囲でLTを一定とおくことが出来るよ
うに, すなわちwとa'の積空間内で,
wとa'の組の分布がゴール近傍の広い範囲で平面的になるように, 部
分空間の基底
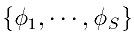 を構成する(図
2.34(b)).
を構成する(図
2.34(b)).
Figure 2.34:
ゴール近傍の広い範囲で, LTを一定とおけるような
部分空間の基底を構成する.
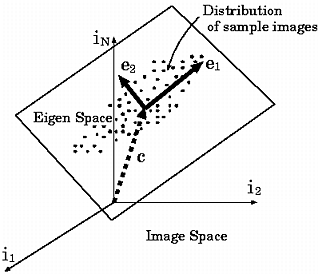 (a) 画像Iを部分空間内でa'と表現する
(a) 画像Iを部分空間内でa'と表現する
|
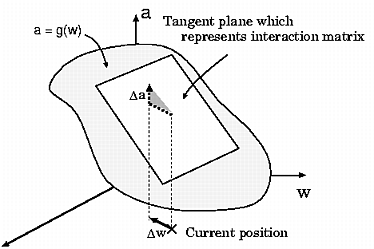 (b) LTによって,a'と
wを対応付ける
(b) LTによって,a'と
wを対応付ける
|
得られた相互行列の疑似逆行列LT+を用いて,
a'のゴールとの違い
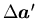 から,
wのゴールとの違い
から,
wのゴールとの違い
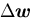 を
を
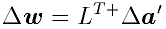 |
(2.5) |
のように推定し, その方向へカメラ・対象物体の運動を制御することで, 視覚
サーボを行う. 以下に, あらかじめ様々な位置で撮影された画像集合
{ I1, …, Ik }
及び, 撮影された位置
{ w1, …, wk }
を用いて, 部分空間の基底
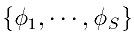 及び, LTを求める方法について述べる.
及び, LTを求める方法について述べる.
固有空間法
まず, 固有空間法により画像を低次元のベクトルで表す. 固有空間法は, 画像
集合の共分散行列の固有ベクトルを部分空間の基底として用いて, 画像を表す
手法である. なお, 表記を単純にするために, 画像を表すベクトル
Iは, あらかじめ画像集合の平均値を引くことで平均
oをとるものとする.
P = [ I1, …, Ik ]
として, 共分散行列Q=PPTのM
組の大きい固有値
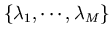 に対
応する固有ベクトル
{ e1, …, eM }を求める.
に対
応する固有ベクトル
{ e1, …, eM }を求める.
固有空間の再構成
次に,
{ e1, …, eM }の線形和により,
式(1)のLTがなるべく
wに依存しないように, 制御基底画像
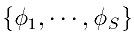 (S < M)を構成する.
(S < M)を構成する.
まず最初に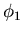 及び,
LT (= [ l1, …,
lS) ]T)
の第1行ベクトルであるl1を決定する.
及び,
LT (= [ l1, …,
lS) ]T)
の第1行ベクトルであるl1を決定する.
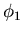 を,
を,
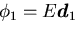 として表す. 画像I
に対する,
として表す. 画像I
に対する, 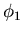 によって得られる係数ベクトルの要素a'1は,
によって得られる係数ベクトルの要素a'1は,
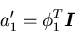 |
(2.6) |
として得られる. a'1を, l1及び,
wのゴールにおける値wGと, ゴール画像
IGに対応するa1'の値
a'1,Gを用いて,
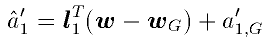 |
(2.7) |
と1次式で推定したときに, 画像集合全体の推定による自乗誤差が小さくなる
ように, l1,
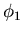 を決定する. 自乗誤差の最小値を与えるl1
,及びその時の平均自乗誤差Errminは,
を決定する. 自乗誤差の最小値を与えるl1
,及びその時の平均自乗誤差Errminは,
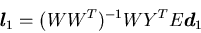 |
(2.8) |
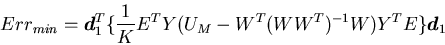 |
(2.9) |
と表現することが出来る. 式(2.9)を小さくすると同時に,
a1'が
wの変化に敏感であるような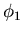 を選びたいので,
a1'の画像集合全体の分散で式(2.9)との比をとる.
を選びたいので,
a1'の画像集合全体の分散で式(2.9)との比をとる.
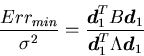 |
(2.10) |
式(2.10)を最小とする,
d1を用いて,
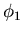 , l1を得る.
d1に直交する条件のもとで, 式
(2.10)を最小にする
d2を求めることで,
, l1を得る.
d1に直交する条件のもとで, 式
(2.10)を最小にする
d2を求めることで,
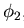 , l2を得る. 以下, 同様にS組の制御基底画像
, l2を得る. 以下, 同様にS組の制御基底画像
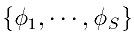 及び, 相互行列
LT (= [ l1, …,
lS) ]T)
を得る.
及び, 相互行列
LT (= [ l1, …,
lS) ]T)
を得る.
制御則
あらかじめ与えられている, ゴール画像の係数ベクトル
a'G
が得られるように制御を行う.
- 1.
- 現在の
wにおける画像Iを得る.
- 2.
- 係数ベクトル
![$ \mbox{\boldmath$a$}' (=[\phi_1,\cdots,\phi_S]^T \mbox{\boldmath$I$})$](img111.gif) を得る.
を得る.
- 3.
-
a'のゴールとの違いから,
wのゴールとの違い
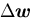 を推定する.
を推定する.
- 4.
- 推定された方向にカメラ・対象物体を少し動かす.
1〜4を繰り返し,
a'が
a'Gと一致したら制御を終了する.



Next: 実験
Up: カメラを搭載したロボットと対象物体の運動の同時制御
Previous: カメラを搭載したロボットと対象物体の運動の同時制御
Contents
wsbmaster@vision.kuee.kyoto-u.ac.jp
![]() に対
応する固有ベクトル
{ e1, …, eM }を求める.
に対
応する固有ベクトル
{ e1, …, eM }を求める.
![]() (S < M)を構成する.
(S < M)を構成する.
![]() 及び,
LT (= [ l1, …,
lS) ]T)
の第1行ベクトルであるl1を決定する.
及び,
LT (= [ l1, …,
lS) ]T)
の第1行ベクトルであるl1を決定する.
![]() を,
を,
![]() として表す. 画像I
に対する,
として表す. 画像I
に対する, ![]() によって得られる係数ベクトルの要素a'1は,
によって得られる係数ベクトルの要素a'1は,
![\begin{displaymath}
\pmatrix{
Y=[ \mbox{\boldmath$I$}_1- \mbox{\boldmath$I$}_G,\...
...oldmath$w$}_K- \mbox{\boldmath$w$}_G]\cr
U_M : M次元単位行列
}
\end{displaymath}](img105.gif)
![\begin{displaymath}
\pmatrix{
B=\frac{1}{K}E^TY(U_M-W^T(WW^T)^{-1}W)Y^TE\cr
\Lambda=\mbox{diag}[\lambda_1,\lambda_2,\cdots,\lambda_M]
}
\end{displaymath}](img107.gif)
![]() , l1を得る.
d1に直交する条件のもとで, 式
(2.10)を最小にする
d2を求めることで,
, l1を得る.
d1に直交する条件のもとで, 式
(2.10)を最小にする
d2を求めることで,
![]() , l2を得る. 以下, 同様にS組の制御基底画像
, l2を得る. 以下, 同様にS組の制御基底画像
![]() 及び, 相互行列
LT (= [ l1, …,
lS) ]T)
を得る.
及び, 相互行列
LT (= [ l1, …,
lS) ]T)
を得る.